Chapter 12 Factor analysis

At this stage, the main objective is to perform an exploratory factor analysis focusing on previous results. The pre-genomic test data analysis allows to identify items that are less relevant and which are the most informative ones, questions with adequate behavior, and how they group. The descriptive analysis of the post-genomic test questionnaire highlighted several common points with the pre-genomic test information, detecting a few conflicting items and the utility of those selected in the previous step. Now, having identified from the pre-genomic test exploratory factor analysis a few key approaches, the aim is to replicate only these factor analyses including the set of items that had been chosen to explore and define how they group in this setting.

12.1 Expectations and concerns domain

One approach is considered including the final set of expectations and concerns items. In this regard, expectations questions include Q2, Q5, Q5, Q7.i, Q7.iv, Q7.v, and all the concerns items. This approach had the best performance in both cohorts, however the matching between VHIO and HOPE was not complete.

12.1.1 Excluding items Q1, Q4, Q7_ii, Q7_iii and Q3.

According to what was defined previously, Q1, Q4, Q7.ii were conflicting, overlapped (Q1 with Q2), with no relevant information, and study dependent (Q7.ii). Then, Q7_iii and Q3 are collecting interesting data but probably they are not related with the other questions in a particular domain; thus, while these items will be included in the questionnaire, they could be excluded from the factor analysis.

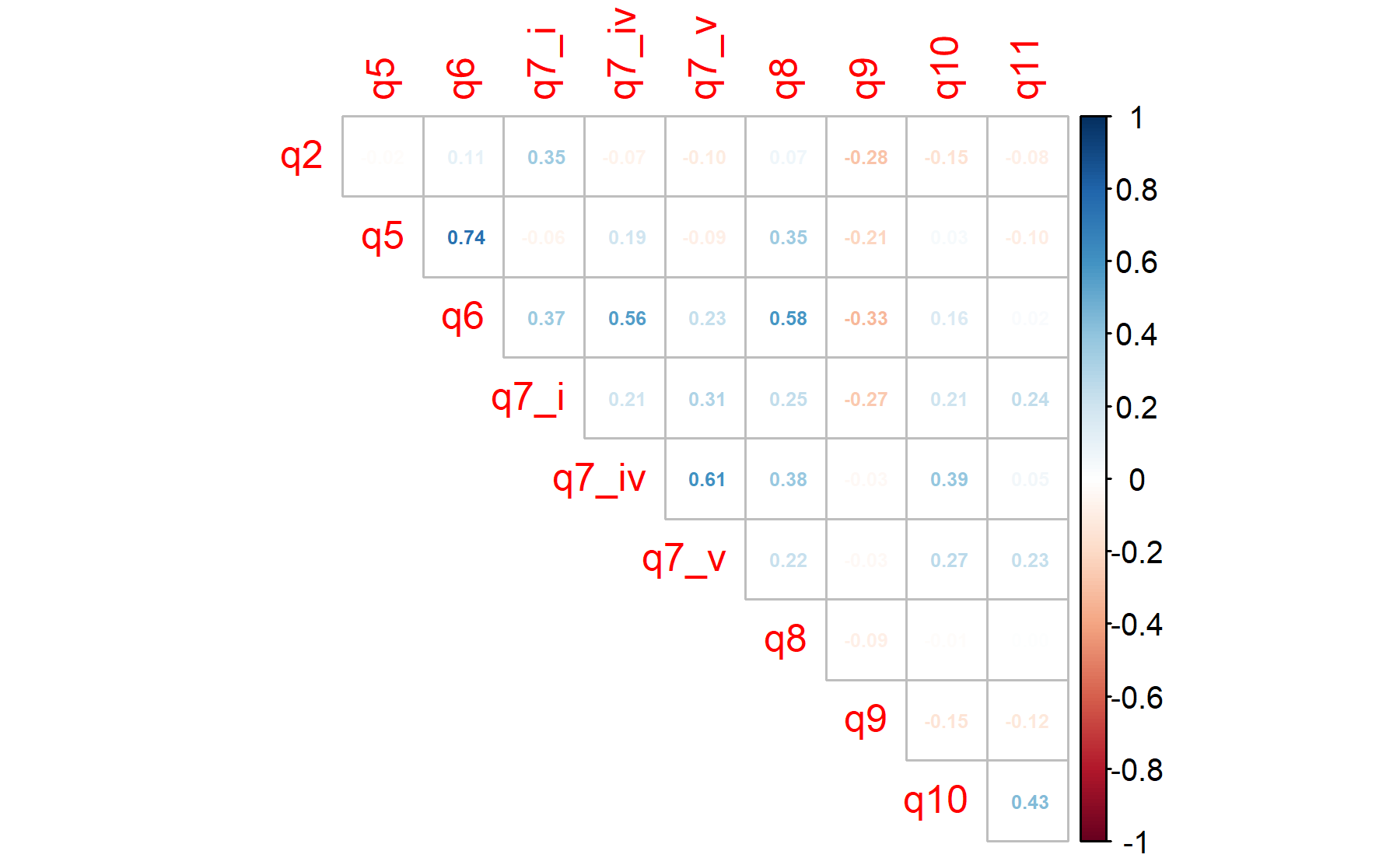
The Barlett’s sphericity test is performed.

Thus, the p-value = 0 and the H0 is rejected confirming the utility of applying a factor analysis to this dataset.

Considering the fact that the Bartlett’s test usually rejects the H0 since the scenario of the null hypothesis is too extreme, the KMO analysis is studied to determine how well the data fit the factor analysis and how useful each item is.

## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = post_test_Q_ExpConcern_facAn_4_corr)
## Overall MSA =  0.5
## MSA for each item = 
##    q2    q5    q6  q7_i q7_iv  q7_v    q8    q9   q10   q11 
##  0.51  0.40  0.49  0.41  0.47  0.61  0.81  0.59  0.49  0.54

According to these results, there are five items below 0.5 (Q5, Q6, Q7.i, Q7.iv, Q10); plus three more below 0.6.

To explore the number of factors PCA is applied. Thus, the table with the PCA results is shown below:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	PC10
Standard deviation	1.7228	1.3391	1.2212	1.0590	0.8612	0.7740	0.6918	0.6848	0.5140	0.2711
Proportion of Variance	0.2968	0.1793	0.1491	0.1121	0.0742	0.0599	0.0479	0.0469	0.0264	0.0073
Cumulative Proportion	0.2968	0.4761	0.6252	0.7374	0.8116	0.8715	0.9193	0.9662	0.9926	1.0000

Then, the scree plot for this PCA analysis is displayed.
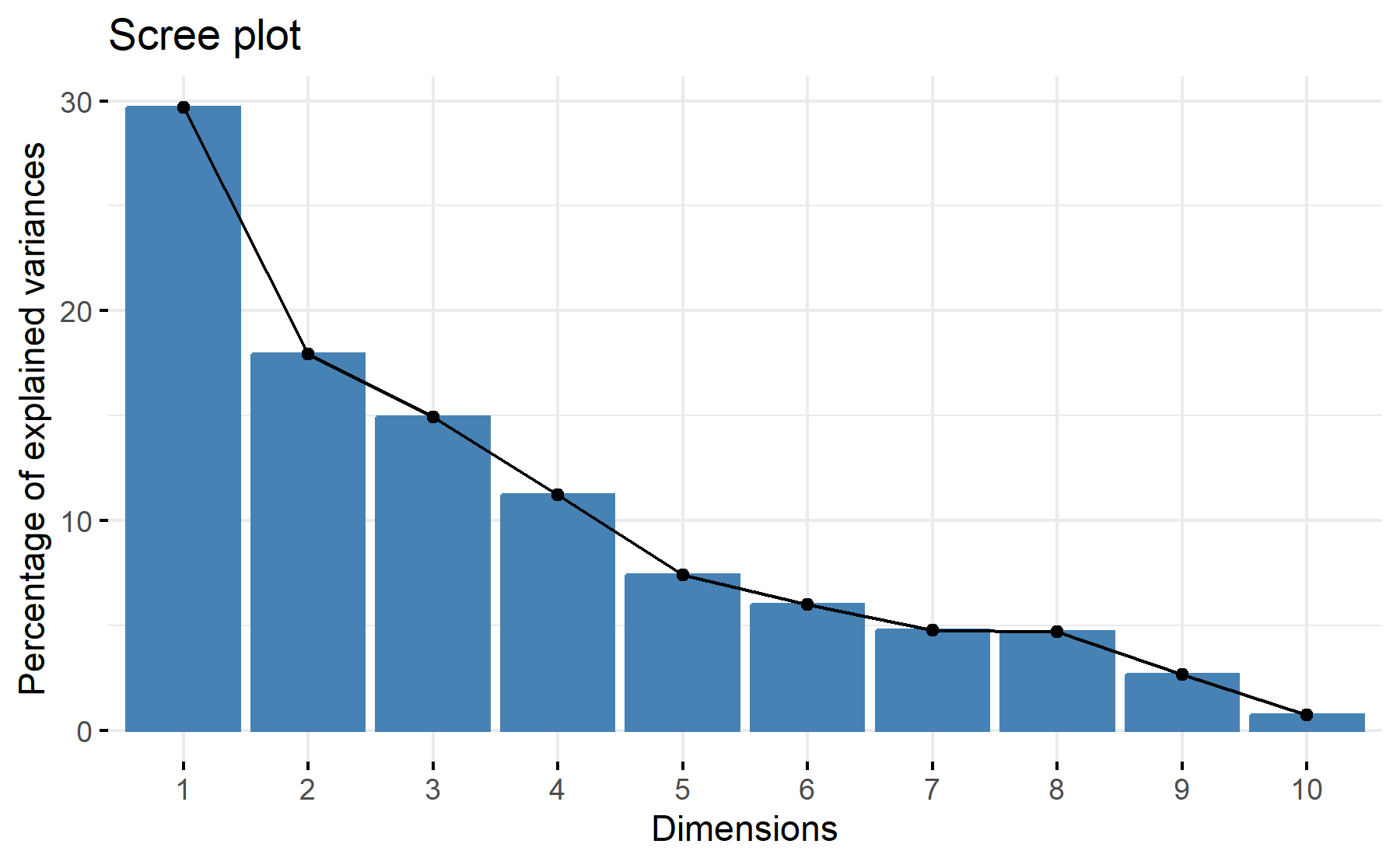According to these results, 3 factors could be the best number with cumulative proportion 63%. However, the greatest elbow is observed on the second component.

Then, another approach is implemented. With this strategy several analysis are combined and depict in the same figure. The tools implemented are: the Kaiser rule (which drops the components with eigenvalues < 1), the parallel analysis, and the usual scree test (plotuScree), the acceleration factor (which indicates where the elbow of the scree plot appears).

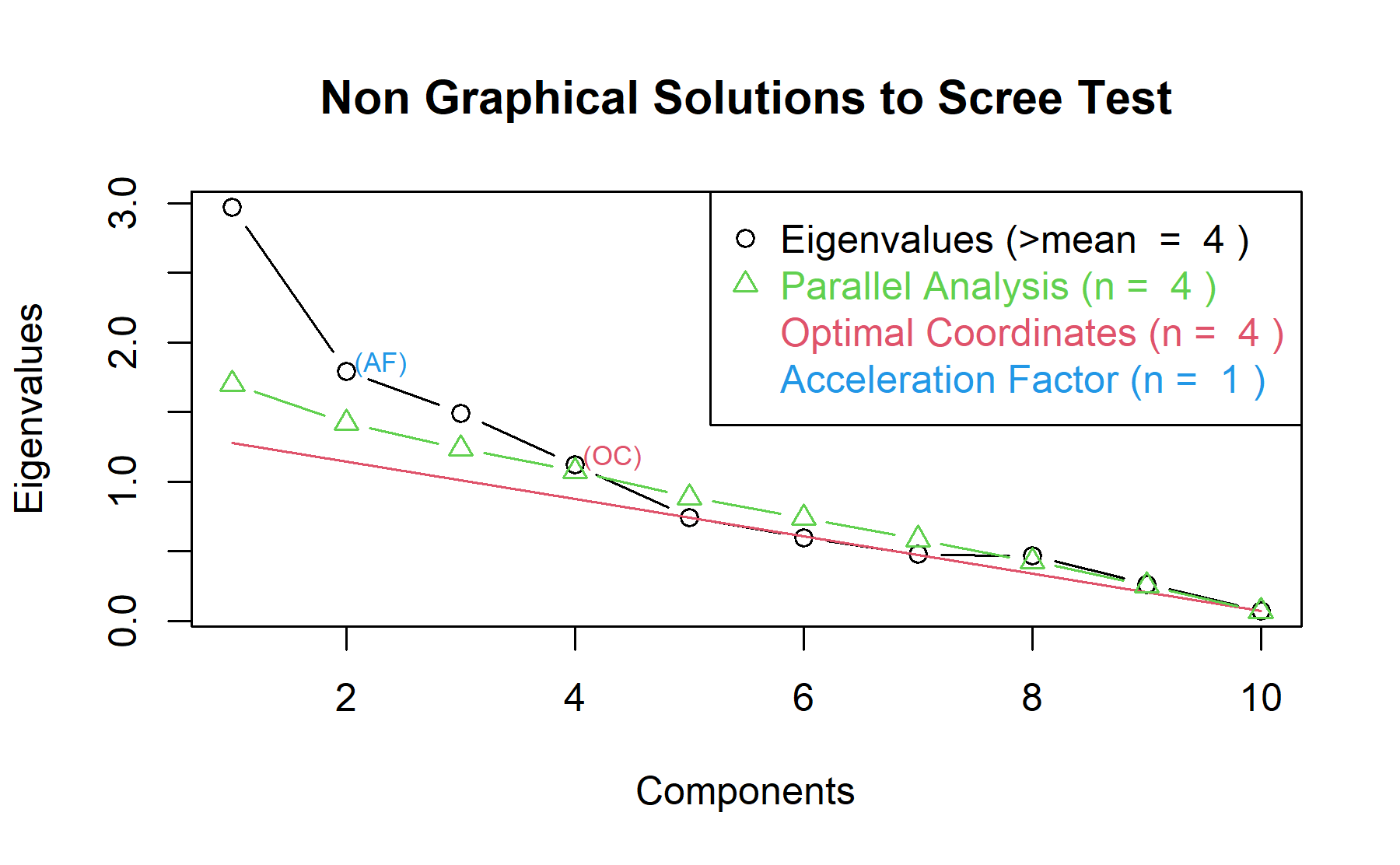Therefore, considering the current analysis four factors seem to be the best choice, however, in the pre-genomic test two factors were identified. Therefore, both approaches will be considered.

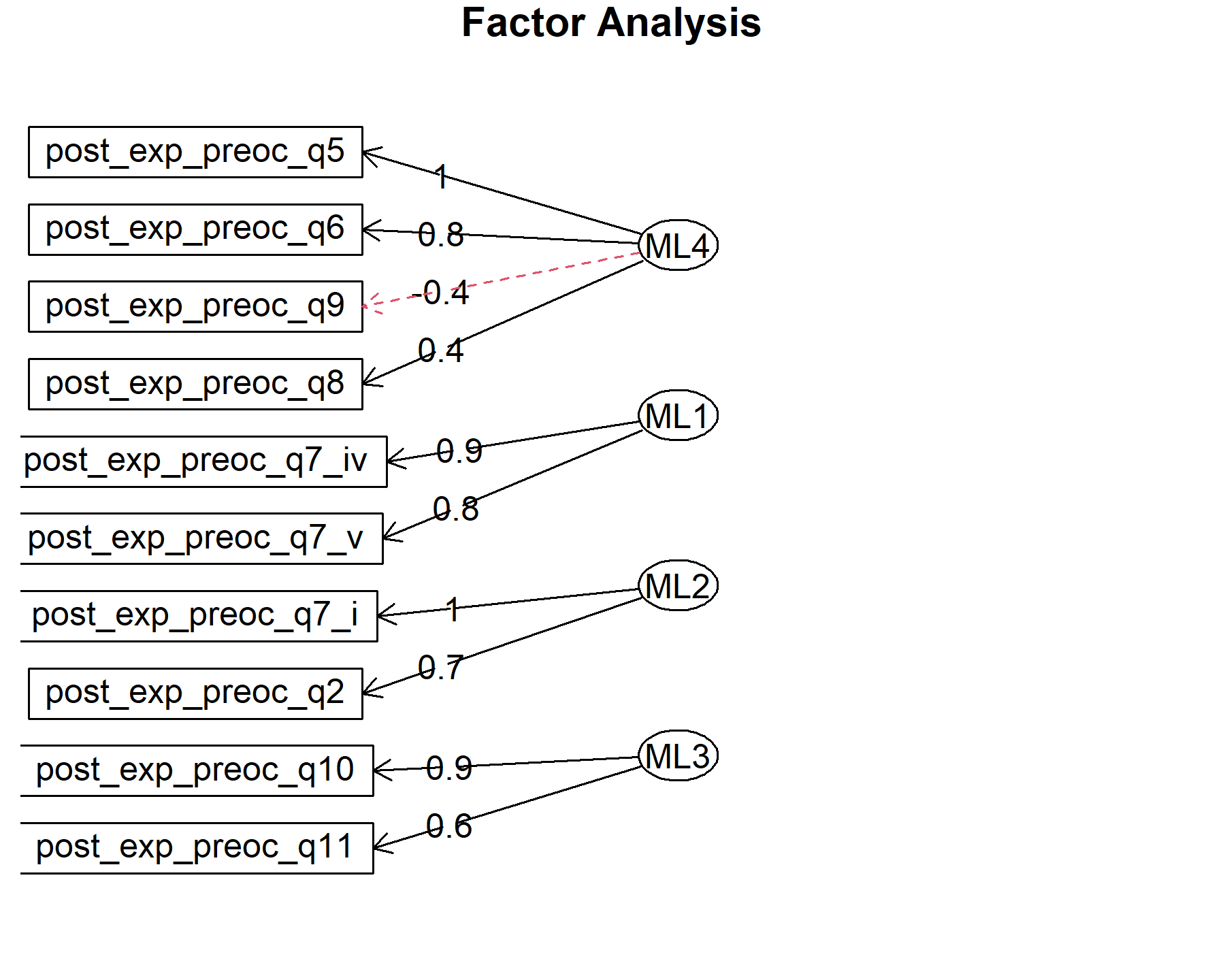
Running the factor analysis with 10 items and 4 factors, first the communalities are explored:

## Warning in cor.smooth(mat): Matrix was not positive definite, smoothing was
## done

## In factor.stats, I could not find the RMSEA upper bound . Sorry about that

##    post_exp_preoc_q2    post_exp_preoc_q5    post_exp_preoc_q6 
##               0.5019               0.8587               0.9950 
##  post_exp_preoc_q7_i post_exp_preoc_q7_iv  post_exp_preoc_q7_v 
##               0.9950               0.9950               0.6126 
##    post_exp_preoc_q8    post_exp_preoc_q9   post_exp_preoc_q10 
##               0.4786               0.3207               0.9950 
##   post_exp_preoc_q11 
##               0.3662

Considering the values of the communalities, all are above 0.3.

Then, the whole output is displayed.

## Factor Analysis using method =  ml
## Call: fa(r = post_test_Q_ExpConcern_facAn_4, nfactors = 4, rotate = "oblimin", 
##     fm = "ml", cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##                        ML4   ML1   ML2   ML3   h2     u2 com
## post_exp_preoc_q2                 0.67       0.50 0.4982 1.4
## post_exp_preoc_q5     0.96                   0.86 0.1413 1.1
## post_exp_preoc_q6     0.82                   1.00 0.0049 1.4
## post_exp_preoc_q7_i               0.98       1.00 0.0050 1.0
## post_exp_preoc_q7_iv        0.85             1.00 0.0049 1.3
## post_exp_preoc_q7_v         0.78             0.61 0.3872 1.2
## post_exp_preoc_q8     0.43                   0.48 0.5214 3.1
## post_exp_preoc_q9    -0.43                   0.32 0.6784 3.2
## post_exp_preoc_q10                      0.94 1.00 0.0050 1.1
## post_exp_preoc_q11                      0.58 0.37 0.6337 1.4
## 
##                        ML4  ML1  ML2  ML3
## SS loadings           2.13 1.77 1.69 1.52
## Proportion Var        0.21 0.18 0.17 0.15
## Cumulative Var        0.21 0.39 0.56 0.71
## Proportion Explained  0.30 0.25 0.24 0.21
## Cumulative Proportion 0.30 0.55 0.79 1.00
## 
##  With factor correlations of 
##      ML4  ML1  ML2  ML3
## ML4 1.00 0.30 0.15 0.06
## ML1 0.30 1.00 0.11 0.30
## ML2 0.15 0.11 1.00 0.10
## ML3 0.06 0.30 0.10 1.00
## 
## Mean item complexity =  1.6
## Test of the hypothesis that 4 factors are sufficient.
## 
## df null model =  45  with the objective function =  26.18 with Chi Square =  650.2
## df of  the model are 11  and the objective function was  19.85 
## 
## The root mean square of the residuals (RMSR) is  0.07 
## The df corrected root mean square of the residuals is  0.15 
## 
## The harmonic n.obs is  30 with the empirical chi square  14.38  with prob <  0.21 
## The total n.obs was  30  with Likelihood Chi Square =  440  with prob <  0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000002 
## 
## Tucker Lewis Index of factoring reliability =  -2.278
## RMSEA index =  1.14  and the 90 % confidence intervals are  1.068 NA
## BIC =  402.6
## Fit based upon off diagonal values = 0.95
## Measures of factor score adequacy             
##                                                    ML4  ML1  ML2  ML3
## Correlation of (regression) scores with factors   1.00 1.00 1.00 1.00
## Multiple R square of scores with factors          0.99 0.99 0.99 0.99
## Minimum correlation of possible factor scores     0.98 0.98 0.99 0.99

There are 4 factors: * Q5, Q6, Q8, Q9. * Q7.iv, Q7.v. * Q2, Q7.i * Q10, Q11. Here, items are split in a different way than in the pre-genomic test, and even regarding the post-test from VHIO (where the number of factors was three).

Finally, plots show the relationship between the items and the factors.

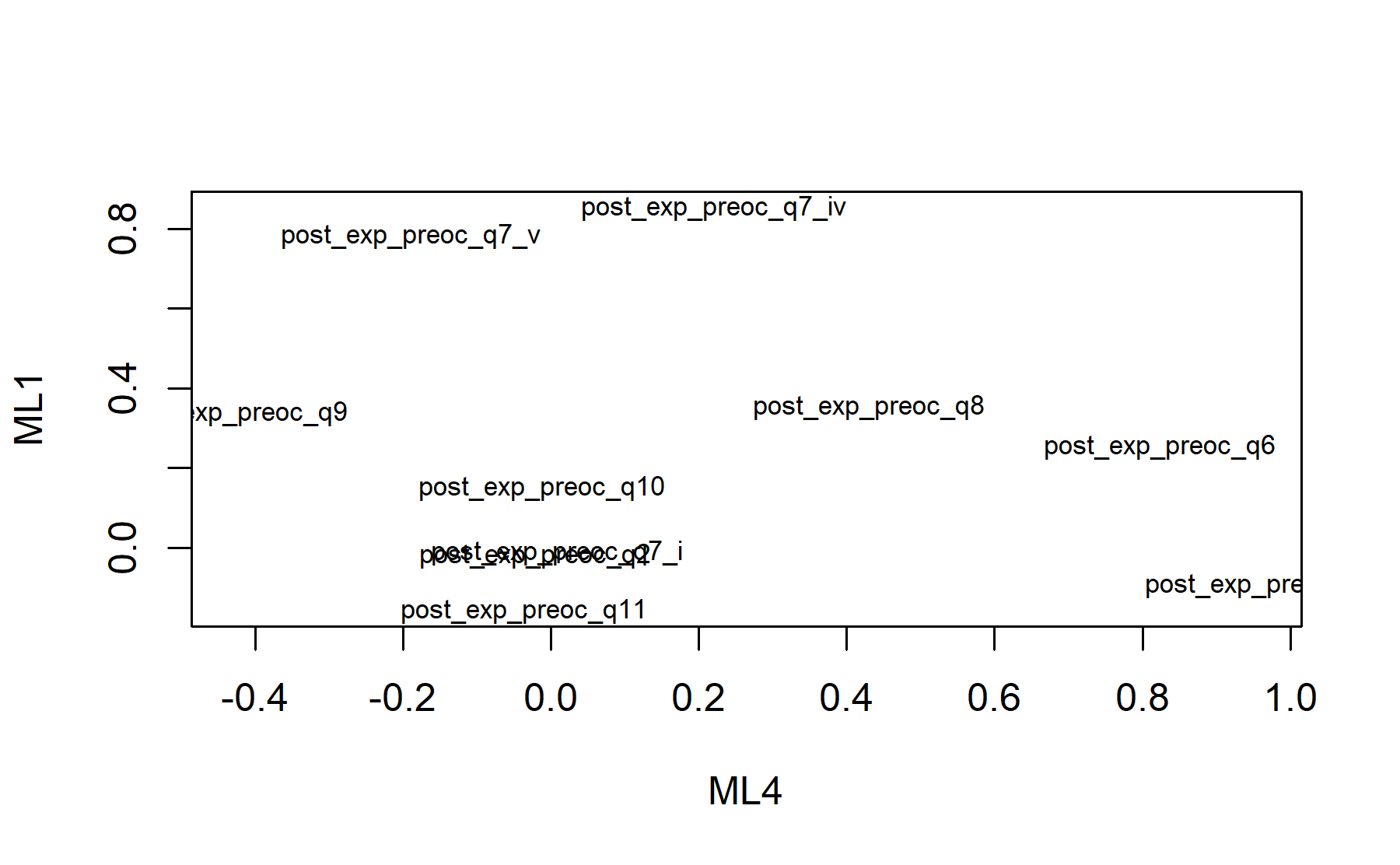
Then, the factor analysis is performed with 2 factors. The communalities are explored:

## Warning in cor.smooth(mat): Matrix was not positive definite, smoothing was
## done

##    post_exp_preoc_q2    post_exp_preoc_q5    post_exp_preoc_q6 
##              0.14223              0.65429              0.99500 
##  post_exp_preoc_q7_i post_exp_preoc_q7_iv  post_exp_preoc_q7_v 
##              0.20531              0.99500              0.52082 
##    post_exp_preoc_q8    post_exp_preoc_q9   post_exp_preoc_q10 
##              0.41338              0.21837              0.34485 
##   post_exp_preoc_q11 
##              0.00913

Considering the values of the communalities, several items show lower communalities (Q2, Q7.i, Q9, and Q11).

Then, the whole output is displayed.

## Factor Analysis using method =  ml
## Call: fa(r = post_test_Q_ExpConcern_facAn_4, nfactors = 2, rotate = "oblimin", 
##     fm = "ml", cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##                        ML1   ML2     h2     u2 com
## post_exp_preoc_q2                0.1433 0.8567 2.0
## post_exp_preoc_q5     0.84       0.6544 0.3456 1.0
## post_exp_preoc_q6     0.93       0.9951 0.0049 1.1
## post_exp_preoc_q7_i   0.49       0.2050 0.7950 1.2
## post_exp_preoc_q7_iv        0.92 0.9950 0.0050 1.1
## post_exp_preoc_q7_v         0.75 0.5208 0.4792 1.0
## post_exp_preoc_q8     0.57       0.4133 0.5867 1.1
## post_exp_preoc_q9    -0.50       0.2175 0.7825 1.5
## post_exp_preoc_q10          0.62 0.3455 0.6545 1.1
## post_exp_preoc_q11               0.0092 0.9908 1.0
## 
##                        ML1  ML2
## SS loadings           2.49 2.01
## Proportion Var        0.25 0.20
## Cumulative Var        0.25 0.45
## Proportion Explained  0.55 0.45
## Cumulative Proportion 0.55 1.00
## 
##  With factor correlations of 
##      ML1  ML2
## ML1 1.00 0.38
## ML2 0.38 1.00
## 
## Mean item complexity =  1.2
## Test of the hypothesis that 2 factors are sufficient.
## 
## df null model =  45  with the objective function =  26.18 with Chi Square =  650.2
## df of  the model are 26  and the objective function was  22.3 
## 
## The root mean square of the residuals (RMSR) is  0.16 
## The df corrected root mean square of the residuals is  0.22 
## 
## The harmonic n.obs is  30 with the empirical chi square  73.5  with prob <  0.000002 
## The total n.obs was  30  with Likelihood Chi Square =  524.1  with prob <  0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000036 
## 
## Tucker Lewis Index of factoring reliability =  -0.511
## RMSEA index =  0.798  and the 90 % confidence intervals are  0.753 0.874
## BIC =  435.6
## Fit based upon off diagonal values = 0.75
## Measures of factor score adequacy             
##                                                    ML1  ML2
## Correlation of (regression) scores with factors   1.00 1.00
## Multiple R square of scores with factors          0.99 0.99
## Minimum correlation of possible factor scores     0.99 0.99

There are 2 factors: * Q5, Q6, Q7.i, Q8, Q9 * Q7.iv, Q7.v, Q10. Out: Q2, Q11 The items are split in a completely different pattern that what was seen in the pre-genomic test questionnaire.

Finally, plots show the relationship between the items and the factors.

12.2 Both domains, the expectations and concerns domain plus the attitudes domain

Now, two other approaches combining expectations and attitudes will be tested, the first one including only the more relevant attitudes items (Q2 and Q3), and the other one considering the four candidates selected from the attitude domain. In both, the same list of previously chosen expectations and concerns items will be used.

12.2.1 Including all the items selected for expectations plus Q2 and Q3 from attitudes.

The Barlett’s sphericity test is performed.

Thus, the p-value = 0 and the H0 is rejected confirming the utility of applying a factor analysis to this dataset.

## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = post_test_Q_Exp_Attit_facAn_1_corr)
## Overall MSA =  0.39
## MSA for each item = 
##           q2           q5           q6         q7_i        q7_iv         q7_v 
##         0.19         0.45         0.46         0.27         0.36         0.34 
##           q8           q9          q10          q11 exp_actit_q2 exp_actit_q3 
##         0.55         0.40         0.32         0.56         0.64         0.34

According to these results, except two, the rest are below 0.5.

To explore the number of factors PCA is applied. Thus, the table with the PCA results is shown below:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	PC10	PC11	PC12
Standard deviation	1.7474	1.5259	1.2398	1.1929	1.0477	0.8210	0.7596	0.7050	0.6284	0.4864	0.3547	0.2348
Proportion of Variance	0.2544	0.1940	0.1281	0.1186	0.0915	0.0562	0.0481	0.0414	0.0329	0.0197	0.0105	0.0046
Cumulative Proportion	0.2544	0.4485	0.5766	0.6952	0.7866	0.8428	0.8909	0.9323	0.9652	0.9849	0.9954	1.0000

Then, the scree plot for this PCA analysis is displayed.
According to these results, 2 or 5 factors could be the best number according to two elbows and the cumulative proportion explained.

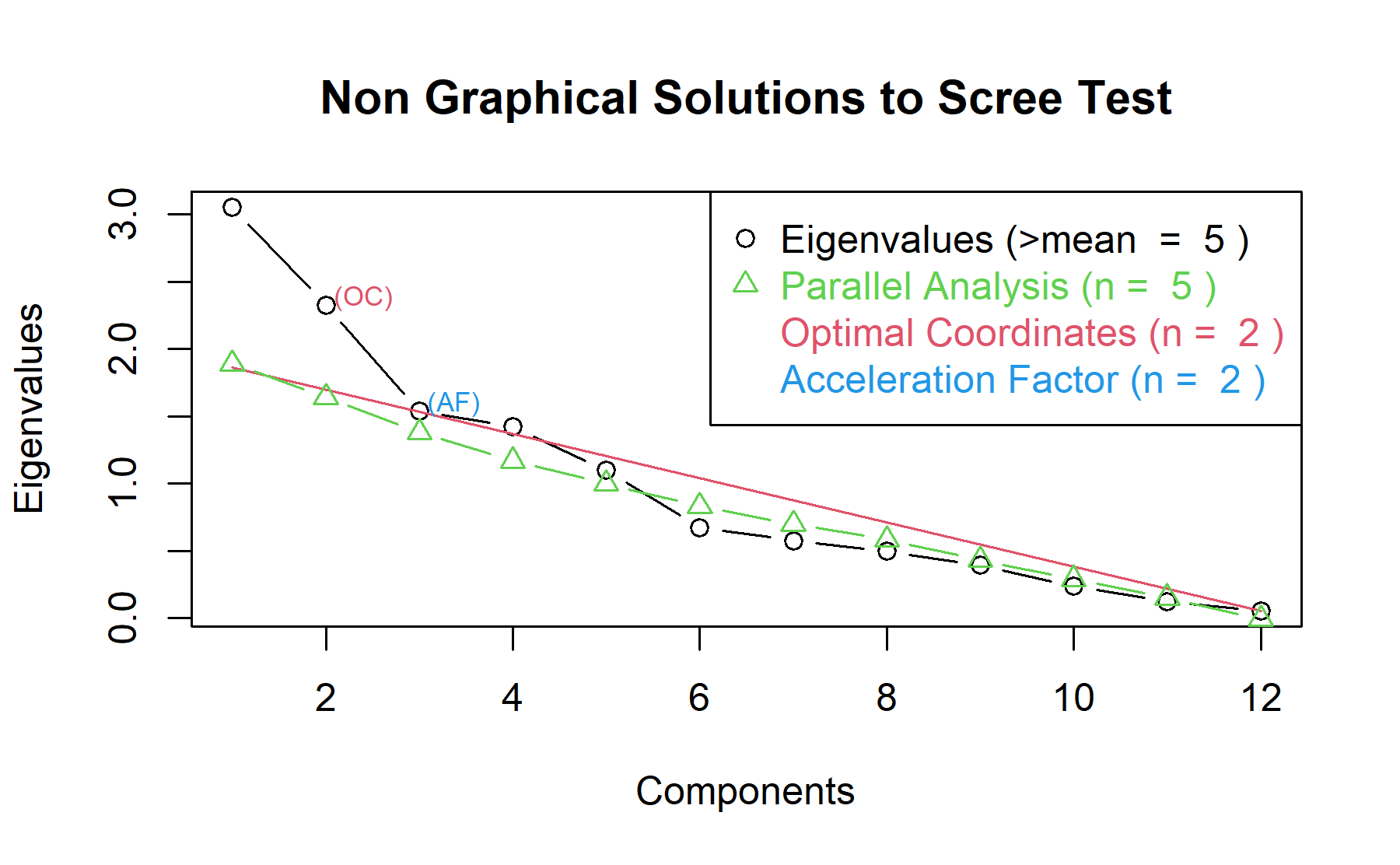Therefore, considering two factors seem to be a possible approach.

Running the factor analysis with 12 items, first the communalities are explored:

## Warning in cor.smooth(mat): Matrix was not positive definite, smoothing was
## done

## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0

## In factor.stats, I could not find the RMSEA upper bound . Sorry about that

##    post_exp_preoc_q2    post_exp_preoc_q5    post_exp_preoc_q6 
##               0.1205               0.6567               0.9950 
##  post_exp_preoc_q7_i post_exp_preoc_q7_iv  post_exp_preoc_q7_v 
##               0.1640               0.4410               0.2459 
##    post_exp_preoc_q8    post_exp_preoc_q9   post_exp_preoc_q10 
##               0.5131               0.1414               0.2286 
##   post_exp_preoc_q11    post_exp_actit_q2    post_exp_actit_q3 
##               0.0311               0.8225               0.9121

Considering the values of the communalities, there some items with low values, such as Q2, Q7.i, Q7.v, Q9, Q10, and Q11.

Then, the whole output is displayed.

## Factor Analysis using method =  ml
## Call: fa(r = post_test_Q_Exp_Attit_facAn_1, nfactors = 2, rotate = "oblimin", 
##     fm = "ml", cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##                        ML1   ML2   h2     u2 com
## post_exp_preoc_q2                0.12 0.8783 1.9
## post_exp_preoc_q5     0.82       0.66 0.3433 1.0
## post_exp_preoc_q6     0.99       1.00 0.0049 1.0
## post_exp_preoc_q7_i              0.16 0.8379 1.0
## post_exp_preoc_q7_iv  0.67       0.44 0.5589 1.1
## post_exp_preoc_q7_v              0.25 0.7544 2.0
## post_exp_preoc_q8     0.58       0.51 0.4867 1.6
## post_exp_preoc_q9                0.14 0.8604 1.1
## post_exp_preoc_q10          0.43 0.23 0.7713 1.6
## post_exp_preoc_q11               0.03 0.9699 1.4
## post_exp_actit_q2           0.81 0.82 0.1775 1.3
## post_exp_actit_q3           0.96 0.91 0.0879 1.0
## 
##                        ML1  ML2
## SS loadings           3.09 2.18
## Proportion Var        0.26 0.18
## Cumulative Var        0.26 0.44
## Proportion Explained  0.59 0.41
## Cumulative Proportion 0.59 1.00
## 
##  With factor correlations of 
##       ML1   ML2
## ML1  1.00 -0.11
## ML2 -0.11  1.00
## 
## Mean item complexity =  1.3
## Test of the hypothesis that 2 factors are sufficient.
## 
## df null model =  66  with the objective function =  49.84 with Chi Square =  1204
## df of  the model are 43  and the objective function was  45.04 
## 
## The root mean square of the residuals (RMSR) is  0.17 
## The df corrected root mean square of the residuals is  0.21 
## 
## The harmonic n.obs is  30 with the empirical chi square  116  with prob <  0.000000012 
## The total n.obs was  30  with Likelihood Chi Square =  1029  with prob <  1.6e-187 
## 
## Tucker Lewis Index of factoring reliability =  -0.411
## RMSEA index =  0.873  and the 90 % confidence intervals are  0.842 NA
## BIC =  882.3
## Fit based upon off diagonal values = 0.71
## Measures of factor score adequacy             
##                                                    ML1  ML2
## Correlation of (regression) scores with factors   1.00 0.97
## Multiple R square of scores with factors          0.99 0.94
## Minimum correlation of possible factor scores     0.99 0.88

There are 2 factors: * Q5, Q6, Q7.iv, Q8. * Q!10, *attQ2, attQ3**.
Several items are left out, such as Q2, Q7.i, Q7.v, Q9, and Q11.

Finally, plots show the relationship between the items and the factors.

12.2.2 Including all the items selected for expectations plus Q2, Q3, Q4, and Q5 inv from attitudes.

The Barlett’s sphericity test is performed.

Thus, the p-value = 0 and the H0 is rejected confirming the utility of applying a factor analysis to this dataset.

## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = post_test_Q_Exp_Attit_facAn_2_corr)
## Overall MSA =  0.35
## MSA for each item = 
##               q2               q5               q6             q7_i 
##             0.17             0.40             0.39             0.20 
##            q7_iv             q7_v               q8               q9 
##             0.37             0.34             0.62             0.26 
##              q10              q11     exp_actit_q2     exp_actit_q3 
##             0.28             0.51             0.53             0.31 
##     exp_actit_q4 exp_actit_q5_Inv 
##             0.60             0.28

According to these results, most of the items are under the threshold of 0.5 (Q2, Q5, Q6, Q7.i, Q7.iv, Q7.v, Q9, Q10, attQ3, and attQ5 inv).

To explore the number of factors PCA is applied. Thus, the table with the PCA results is shown below:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	PC10	PC11	PC12	PC13	PC14
Standard deviation	1.7940	1.5648	1.3892	1.2284	1.0634	0.9443	0.8838	0.7668	0.7191	0.6267	0.4900	0.4377	0.3504	0.1947
Proportion of Variance	0.2299	0.1749	0.1378	0.1078	0.0808	0.0637	0.0558	0.0420	0.0369	0.0281	0.0171	0.0137	0.0088	0.0027
Cumulative Proportion	0.2299	0.4048	0.5426	0.6504	0.7312	0.7949	0.8507	0.8927	0.9296	0.9577	0.9748	0.9885	0.9973	1.0000

Then, the scree plot for this PCA analysis is displayed.
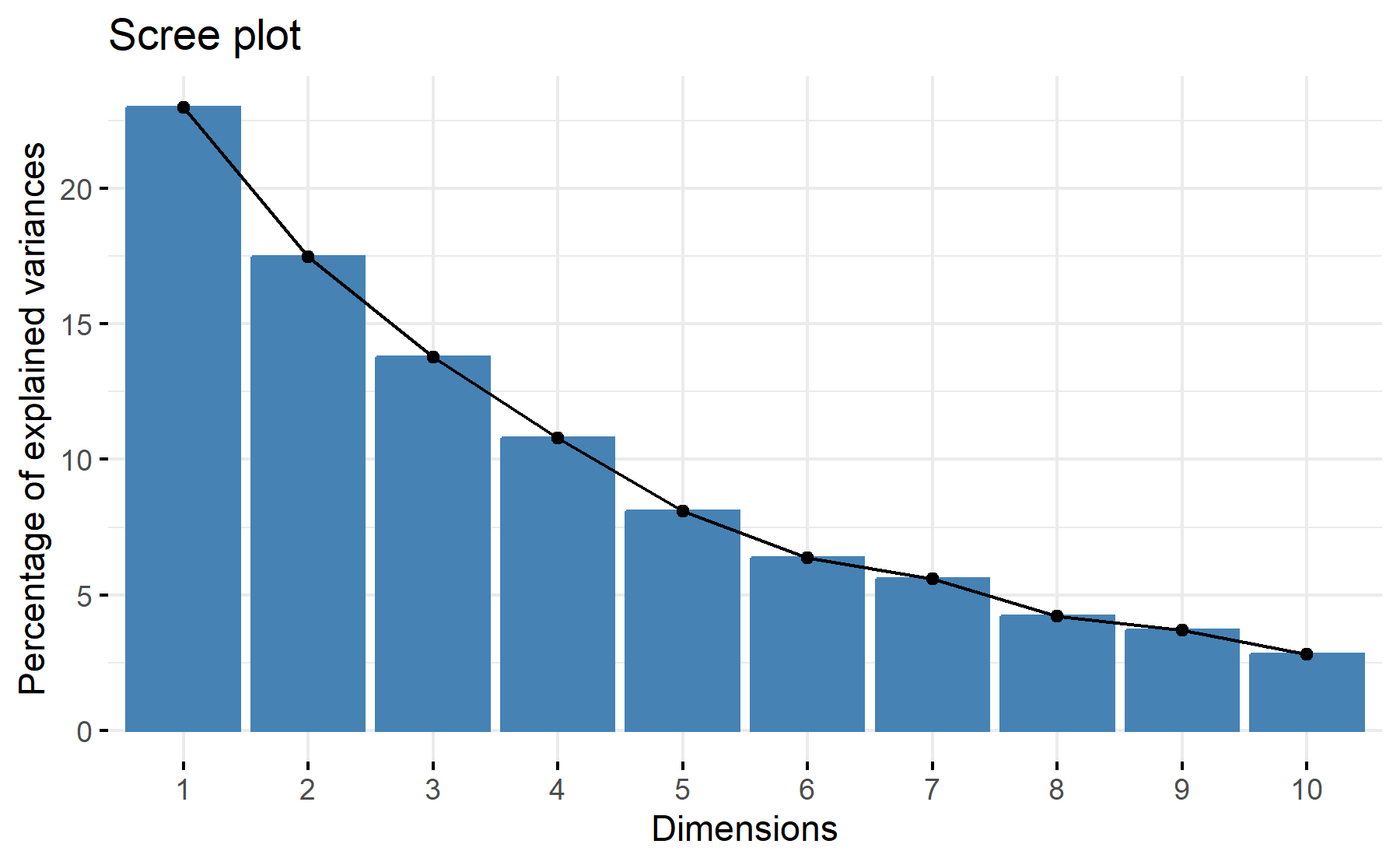According to these results, there is no a clear elbow. The cumulative proportion for 3 components is 54%.

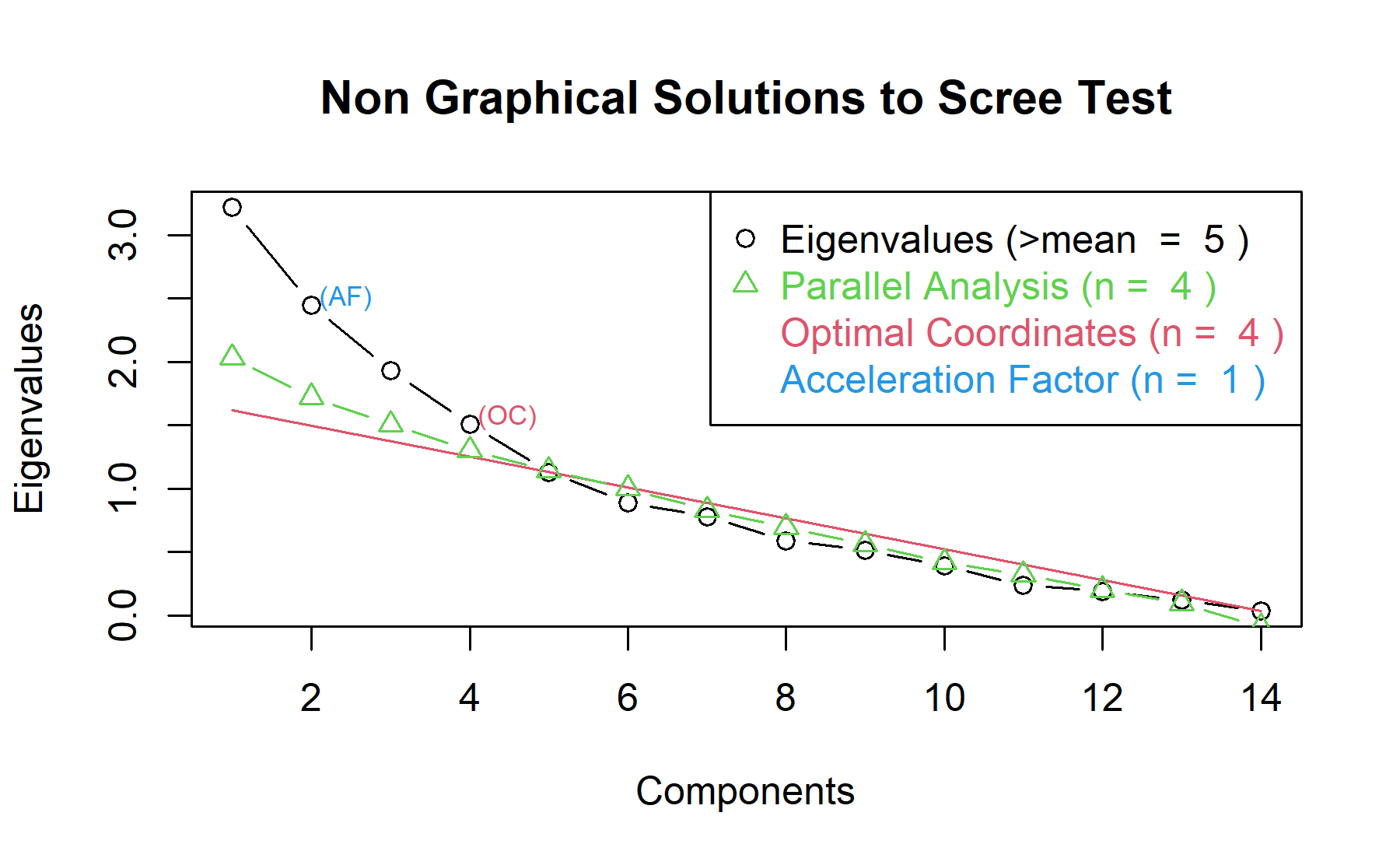Three factors are condidered to emulate the number in the pre-genomic test. Nevertheless, according to these analyses, 1,4, and 5 could be adequate number of factors.

Running the factor analysis with 14 items, first the communalities are explored:

## Warning in cor.smooth(mat): Matrix was not positive definite, smoothing was
## done

## In smc, smcs < 0 were set to .0
## In smc, smcs < 0 were set to .0

## In factor.stats, I could not find the RMSEA upper bound . Sorry about that

##          post_exp_preoc_q2          post_exp_preoc_q5 
##                    0.33083                    0.72843 
##          post_exp_preoc_q6        post_exp_preoc_q7_i 
##                    0.99500                    0.19401 
##       post_exp_preoc_q7_iv        post_exp_preoc_q7_v 
##                    0.99500                    0.53906 
##          post_exp_preoc_q8          post_exp_preoc_q9 
##                    0.51352                    0.24376 
##         post_exp_preoc_q10         post_exp_preoc_q11 
##                    0.41381                    0.03147 
##          post_exp_actit_q2          post_exp_actit_q3 
##                    0.72004                    0.99500 
##          post_exp_actit_q4 post_exp_actit_q5_Inverted 
##                    0.45031                    0.30621

Considering the values of the communalities, two have values below 0.3 (Q7.i, Q11, and Q9).

Then, the whole output is displayed.

## Factor Analysis using method =  ml
## Call: fa(r = post_test_Q_Exp_Attit_facAn_2, nfactors = 3, rotate = "oblimin", 
##     fm = "ml", cor = "poly")
## Standardized loadings (pattern matrix) based upon correlation matrix
##                              ML3   ML2   ML1   h2     u2 com
## post_exp_preoc_q2           0.47             0.33 0.6690 2.8
## post_exp_preoc_q5           0.87             0.73 0.2716 1.0
## post_exp_preoc_q6           0.86             1.00 0.0049 1.2
## post_exp_preoc_q7_i         0.45             0.19 0.8062 1.2
## post_exp_preoc_q7_iv                    0.95 1.00 0.0050 1.0
## post_exp_preoc_q7_v                     0.70 0.54 0.4610 1.3
## post_exp_preoc_q8           0.45             0.51 0.4864 2.5
## post_exp_preoc_q9          -0.52             0.24 0.7565 1.5
## post_exp_preoc_q10                      0.56 0.41 0.5864 1.6
## post_exp_preoc_q11                           0.03 0.9697 1.8
## post_exp_actit_q2                 0.77       0.72 0.2800 1.3
## post_exp_actit_q3                 0.99       1.00 0.0050 1.0
## post_exp_actit_q4                 0.55       0.45 0.5498 1.8
## post_exp_actit_q5_Inverted                   0.31 0.6936 2.1
## 
##                        ML3  ML2  ML1
## SS loadings           2.69 2.50 2.26
## Proportion Var        0.19 0.18 0.16
## Cumulative Var        0.19 0.37 0.53
## Proportion Explained  0.36 0.34 0.30
## Cumulative Proportion 0.36 0.70 1.00
## 
##  With factor correlations of 
##       ML3   ML2  ML1
## ML3  1.00 -0.07 0.35
## ML2 -0.07  1.00 0.03
## ML1  0.35  0.03 1.00
## 
## Mean item complexity =  1.6
## Test of the hypothesis that 3 factors are sufficient.
## 
## df null model =  91  with the objective function =  71.58 with Chi Square =  1682
## df of  the model are 52  and the objective function was  64.54 
## 
## The root mean square of the residuals (RMSR) is  0.13 
## The df corrected root mean square of the residuals is  0.17 
## 
## The harmonic n.obs is  30 with the empirical chi square  90.8  with prob <  0.0007 
## The total n.obs was  30  with Likelihood Chi Square =  1388  with prob <  3.4e-256 
## 
## Tucker Lewis Index of factoring reliability =  -0.614
## RMSEA index =  0.925  and the 90 % confidence intervals are  0.899 NA
## BIC =  1211
## Fit based upon off diagonal values = 0.82
## Measures of factor score adequacy             
##                                                    ML3  ML2  ML1
## Correlation of (regression) scores with factors   1.00 1.00 1.00
## Multiple R square of scores with factors          0.99 1.00 0.99
## Minimum correlation of possible factor scores     0.99 0.99 0.99

There are 3 factors: * Q2, Q5, Q6, Q7.i, Q8, -Q9.
* Q7.iv, Q7.v, Q10. * attQ2, attQ3, attQ4.

There are two items out: attQ4 inv, and Q11.

Finally, plots show the relationship between the items and the factors.

12.3 Global conclusions

In this setting, the exploratory factor analysis does not match with the analysis of the pre-genomic test. Items did not group in a similar way the pre questionnaire and here. While the questions are similar and no identical, the change between before and after could modify the underling meaning or the general behavior of the tool itself.